攻克高考数学难点,拿下直线与圆锥有关的综合
 直线与圆锥曲线相关问题,我们大体可以分为这么几类:直线与椭圆、双曲线、抛物线的位置关系等。直线与圆锥曲线作为高考数学一个必考的重难点,会重点考查学生对数形结合、分类讨论、函数与方程、等价转化等数学思想方法的掌握情况,凸显高考数学选拔人才的功能。
直线与圆锥曲线相关问题,我们大体可以分为这么几类:直线与椭圆、双曲线、抛物线的位置关系等。直线与圆锥曲线作为高考数学一个必考的重难点,会重点考查学生对数形结合、分类讨论、函数与方程、等价转化等数学思想方法的掌握情况,凸显高考数学选拔人才的功能。
直线与椭圆位置关系的进行判断,如一般都是将直线的方程和椭圆的方程联立,通过讨论此方程组的实数解的组数来确定,即用消元后的关于x(或y)的一元二次方程的判断式Δ的符号来确定:
1.当Δ>0时,直线和椭圆相交;
2.当Δ=0时,直线和椭圆相切;
3.当Δ
直线与椭圆的位置关系作为椭圆当中最为复杂的综合问题,常常与平面几何、直线方程与两直线的位置关系、圆、平面向量、函数最值、方程、不等式等知识进行联系,增强知识的应用层面。这些综合变化都对考生的数学能力提出挑战,如考生在平时数学学习过程中,要大力提高自身的字母运算能力、逻辑推理能力、语言转化能力、数形转化能力等。
 直线与椭圆有关的高考试题分析,典型例题1:
直线与椭圆有关的高考试题分析,典型例题1:
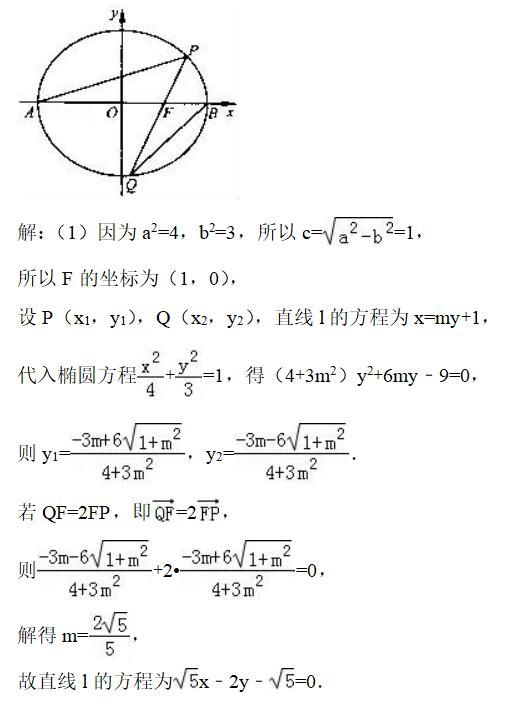
如图,在平面直角坐标系xOy中,已知椭圆C:x2/4+y2/3=1的左、右顶点分别为A,B,过右焦点F的直线l与椭圆C交于P,Q两点(点P在x轴上方).
(1)若QF=2FP,求直线l的方程;
(2)设直线AP,BQ的斜率分别为k?,k?,是否存在常数λ,使得k?=λk??若存在,求出λ的值;若不存在,请说明理由.
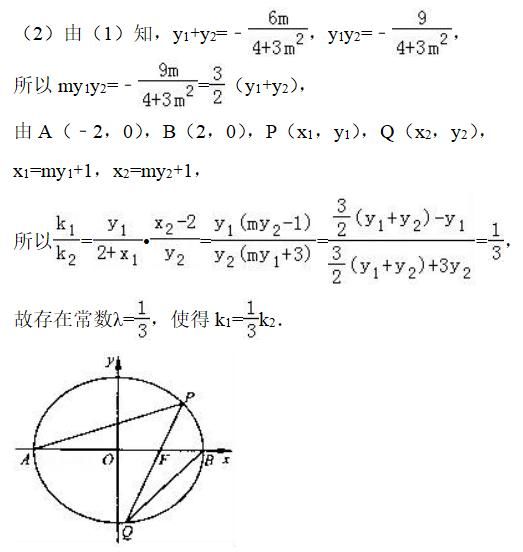 考点分析:
考点分析:
直线与椭圆的位置关系.
题干分析:
(1)由椭圆方程求出a,b,c,可得F的坐标,设P(x?,y?),Q(x?,y?),直线l的方程为x=my+1,代入椭圆方程,求得P,Q的纵坐标,再由向量共线的坐标表示,可得m的方程,解方程可得m,进而得到直线l的方程;
(2)运用韦达定理可得y?+y?,y?y?,my?y2,由A(﹣2,0),B(2,0),P(x?,y?),Q(x?,y?),x?=my?+1,x?=my?+1,运用直线的斜率公式,化简整理计算可得常数λ的值,即可判断存在.
 直线与椭圆有关的高考试题分析,典型例题2:
直线与椭圆有关的高考试题分析,典型例题2:
在平面直角坐标系xOy中,已知椭圆x2/a2+y2/b2=1(a>b>0)的左焦点为F(﹣1,0),且经过点(1,3/2).
(1)求椭圆的标准方程;
(2)已知椭圆的弦AB过点F,且与x轴不垂直.若D为x轴上的一点,DA=DB,求AB/DF的值.

 考点分析:
考点分析:
直线与椭圆的位置关系.
题干分析:
(1)根据椭圆的定义,即可求得2a=4,由c=1,b2=a2﹣c2=3,即可求得椭圆的标准方程;
(2)分类讨论,当直线的斜率存在时,代入椭圆方程,由韦达定理及中点坐标公式求得M点坐标,求得直线AB垂直平分线方程,即可求得D点坐标,由椭圆的第二定义,求得丨AF丨=(x1+4)/2,即丨BF丨=(x2+4)/2,利用韦达定理即可求得丨AB丨,即可求得丨AB丨/丨DF丨的值.
 直线与椭圆有关的高考试题分析,典型例题3:
直线与椭圆有关的高考试题分析,典型例题3:
已知椭圆C:x2/a2+y2/b2=1(a>b>0)的短轴长为2,且函数y=x2﹣65/16的图象与椭圆C仅有两个公共点,过原点的直线l与椭圆C交于M,N两点.
(1)求椭圆C的标准方程;
(2)点P为线段MN的中垂线与椭圆C的一个公共点,求△PMN面积的最小值,并求此时直线l的方程.

 考点分析:
考点分析:
直线与椭圆的位置关系.
题干分析:
(1)由题意可得:2b=2,解得b=1.联立x2/a2+y2=1(a>1)与y=x2﹣65/16,可得:x4+(1/a2-65/8)x2+81×49/162=0,根据椭圆C与抛物线y=x2﹣65/16的对称性,可得:△=0,a>1,解得a.
(2)①当直线l的斜率不存在时,S△PMN=1/2×2b×a;当直线l的斜率为0时,S△PMN=1/2×2b×a.
②当直线l的斜率存在且不为0时,设直线l的方程为:y=kx,与椭圆方程联立解得x2,y2.|MN|=2√(x2+y2).由题意可得:线段MN的中垂线方程为:y=﹣x/k,与椭圆方程联立可得|OP|=√(x2+y2).利用S△PMN=1/2×|MN|×|OP|,与基本不等式的性质即可得出。
