学物理也要用到基础数学《张朝阳的物理课》推
2月20日12时,《张朝阳的物理课》第三十期开播。搜狐创始人、董事局主席兼CEO张朝阳坐镇搜狐视频直播间。他先带着网友复习麦克斯韦速度分布律,补充了速度分布化为速率分布的细节,引出关于直角坐标系与球坐标系的讨论,并导出球坐标系的体积元。之后以球壳与质点间的引力计算为例,结合巧妙的积分参数变换,得到具体公式,最终发现球壳所受引力可以等效到其质心上,即质量集中到球心。将球壳积分变为球体也具有同样的结论。

“今天是复习和反刍的一天。”张朝阳说,“上节课谈了玻尔兹曼在速度场和重力场的分布,今天本来想讲点玻尔兹曼分布更普遍的证明,但比它更重要的,是组合与熵的概念。这样就得学点热力学、学点数学,补充点基础知识。”
区别与联系:麦克斯韦速度分布与速率分布
张朝阳先带着网友复习如何推导麦克斯韦速度分布。“它重点强调理想气体的各向同性,表明速度分布只与速率有关。”他解释说,依据三个垂直方向上速度分布的独立性,可以将总的速度分布函数分解为各个方向上速度分布函数的乘积;之后取对数,将乘积化为求和的形式,再对某一速度分量求偏导;结合一些简单的变换,就可以用分离变量法,解出各方向上的速度分布,进而回过头来,得到完整的三维速度分布。
利用球坐标系与直角坐标系中体积微元之间的关系,可将速度分布化为速率分布。张朝阳指出,“速率分布显示,粒子速率趋于0时,概率密度趋于0。然而,速度分布却显示,粒子在某方向上的速度为0时,概率密度取到最大值。”
怎么理解这个看似矛盾的结果呢?张朝阳解释说,速度分布描述的是,速度处在速度区间Vx~Vx+dVx、Vy~Vy+dVy、Vz~Vz+dVz的粒子数,它对x、y、z三个分量都有要求,只要其中一个速度分量超出此区间,就不计算在分布里面。但是,速率分布描述的是速率处在速率区间V~V+dV的粒子数。由速率与速度的定义,可以知道他们并不是一一对应的。一个速率可以对应多个速度。一个速度区间A的粒子,对相应的速率区间dV有贡献;但速率区间dV,包含的不只有速度区间A的粒子,还包含了其它速度区间B、C、D等的粒子。由速率与速度之间的关系,可以看出,当速率越小,其在球坐标系对应的球面越小,直观来讲就是对应的可取速度状态数越少。所以,即使速度分布在各自速度分量趋于0时能取到最大值,对速率分布,当速率趋于0时,对应的状态数急剧下降,概率密度趋于0。
如何定量描述速率区间与速度区间状态数的对应关系呢?张朝阳告诉网友,“这就涉及到球坐标系体积微元的推导。”
几何与变换:球坐标系的体积微元
张朝阳对着示意图边写公式边推导。他说,在球坐标(r,θ,φ)所示的某点上,给θ做一个微小的变化dθ,同时也给φ做一个微小的变化dφ,就会在半径为r的球面上,划出一个边长分别为rdθ 与rsinθdφ的小面积元,其面积大小为r^2sinθdθdφ,若对r再做个微小的变化dr,则会形成一个以前述面积元为底、高度为dr的体积微元,其体积大小是r^2sinθdθdφdr,这就是球坐标区间θ~θ+dθ、φ~φ+dφ、r~r+dr所对应的体积。
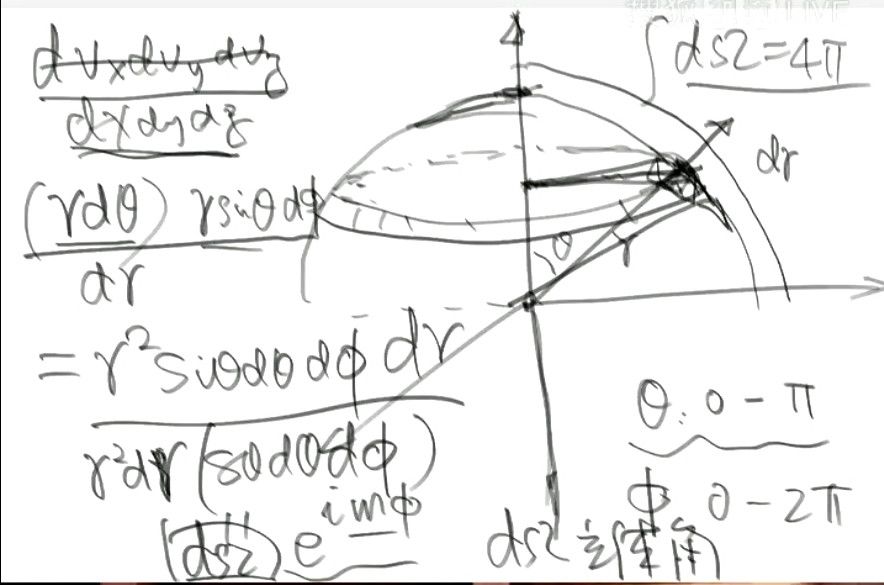
(推导球坐标系的体积元)
在笛卡尔坐标系里,体积微元是dxdydz;将积分变量从直角坐标系变换到球坐标系后,就可以将直角坐标的体积微元换成r^2sinθdθdφdr再继续积分。当然,类似地,反过来从球坐标到直角坐标也是可以进行变换的。
同理,将x,y,z换成速度Vx,Vy,Vz,速度区间所示的体积微元dVxdVydVz对应到球坐标系里的体积微元就是V^2sinθdθdφdV,其中V是速率。所以当速率趋于零时,体积元以V^2方式减小到零,这就解释了为什么速率趋于零时对应的速率分布值也趋于零。
分割、换元、组合、等效:计算均匀球体的引力
作为球坐标系的一个典型应用,现在计算质量为m的质点与半径为r的球壳之间的引力,质点与球心的距离为R,具体参数如下图所示:

(张朝阳巧妙选取积分变量计算球壳与质点的引力)
张朝阳继续说明,“设球壳密度为ρ,半径为r的球壳上的小体积元质量为ρr^2sinθdθdφdr,其与质点的距离设为l,则球壳与质点m之间的引力为:”
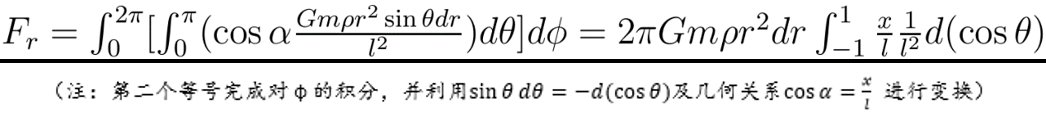
如果将x与l表示为cosθ的函数,积分会变得比较难,故尝试选取其它参量作为积分变量。注意到cosθ可由其所在的直角三角形的边长表示为:
